OBJECTIF
Je veux montrer qu'une propriété est vraie pour tout nombre entier naturel !
Comment faire ?
J'utilise le raisonnement par récurrence !
OBJET
J'ai besoin d'une propriété définie sur l'ensemble des nombres entiers naturels !
Je prends la propriété
\(P\big(\color{dodgerblue}{n}\big)\)
avec \(\color{dodgerblue}{n\in\mathbb{N}}\) .
Rang de la propriété
Propriété \(\color{deeppink}{P}\)
Rang \(0\)
➜
\(P\big(\color{dodgerblue}{0}\big)\)
Rang \(\color{dodgerblue}{1}\)
➜
\(P\big(\color{dodgerblue}{1}\big)\)
Rang \(\color{dodgerblue}{2}\)
➜
\(P\big(\color{dodgerblue}{2}\big)\)
Rang \(\color{dodgerblue}{3}\)
➜
\(P\big(\color{dodgerblue}{3}\big)\)
...
...
Rang \(\color{dodgerblue}{k}\)
➜
\(P\big(\color{dodgerblue}{k}\big)\)
Rang \(\color{dodgerblue}{k+1}\)
➜
\(P\big(\color{dodgerblue}{k+1}\big)\)
...
...
METHODE
Le raisonnement par récurrence se construit en 3 étapes.
Etape 1
Initialisation
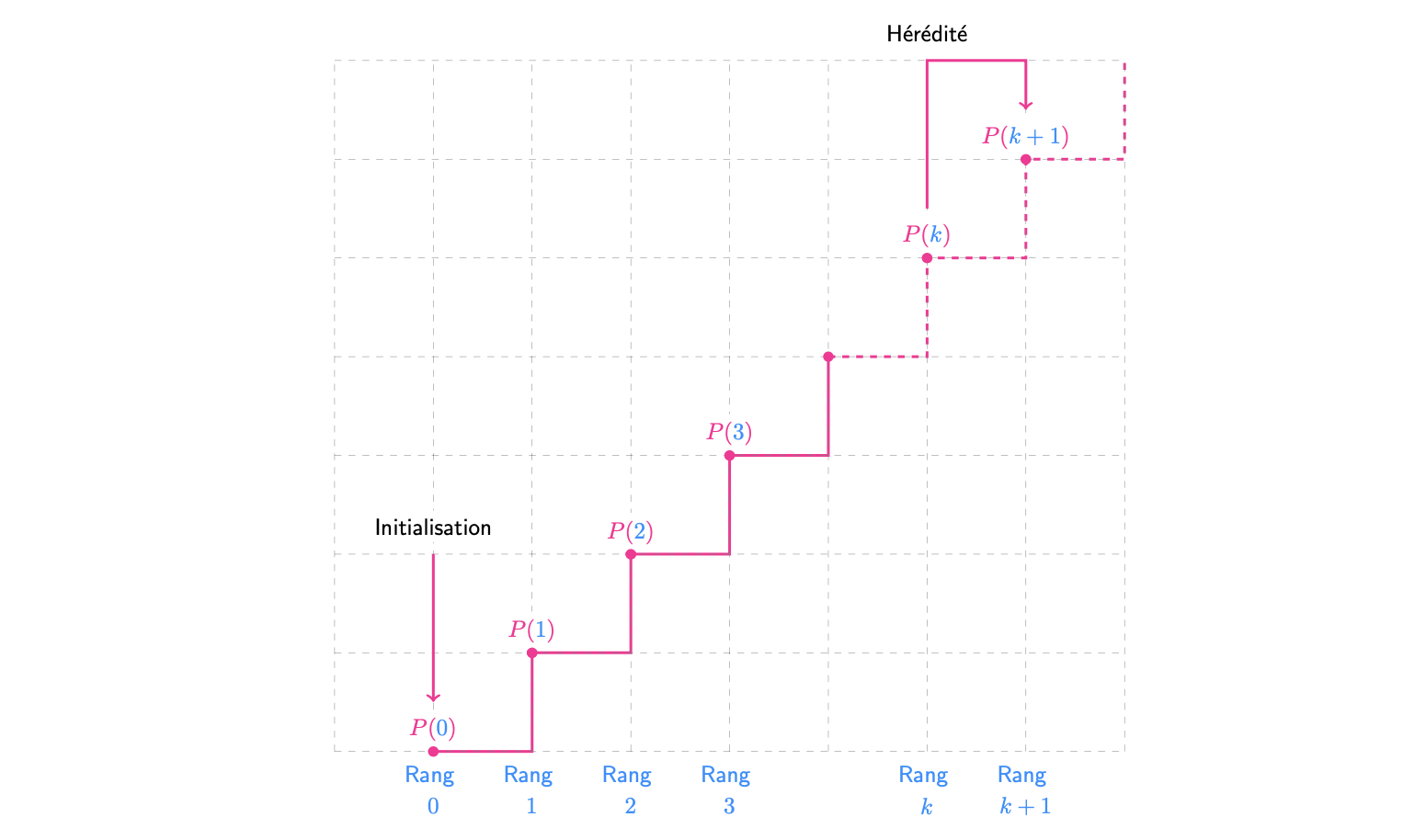
L'initialisation est le point de départ du raisonnement.
C'est l'étape de vérification du rang initial de la propriété.
Je montre que
la propriété \(\color{deeppink}{P}\) est vraie au rang initial.
Le rang initial dépend de la définition de la propriété.
Ici la propriété \(\color{deeppink}{P}\) est définie pour tout nombre entier naturel \(\color{dodgerblue}{n\geq 0}\)
alors le rang initial de \(\color{deeppink}{P}\) est \(\color{dodgerblue}{0}\)
et donc
je montre que \(P\big(\color{dodgerblue}{0}\big)\) est vraie.
Autres exemples
(1) Si la propriété est définie pour tout nombre entier naturel \(\color{dodgerblue}{n\geq 1}\)
alors le rang initial de \(\color{deeppink}{P}\) est \(\color{dodgerblue}{1}\)
et donc
je montre que \(\color{deeppink}{P\big(\color{dodgerblue}{1}\big)}\) est vraie.
(2) Si la propriété est définie pour tout nombre entier naturel \(\color{dodgerblue}{n\geq 2}\)
alors le rang initial de \(\color{deeppink}{P}\) est \(\color{dodgerblue}{2}\)
et donc
je montre que \(P\big(\color{dodgerblue}{2}\big)\) est vraie.
etc..
Etape 2
Hérédité

Je montre que
si \(\color{deeppink}{P}\) est vraie au rang \(\color{dodgerblue}{k}\)
alors
\(\color{deeppink}{P}\) est vraie au rang \(\color{dodgerblue}{k+1}\) .
Autrement dit,
je suppose que la propriété est vraie au rang \(\color{dodgerblue}{k}\)
et à partir de cette supposition,
(que l'on appelle hypothèse de récurrence)
je montre que la propriété est vraie au rang \(\color{dodgerblue}{k+1}\).
Etape 3
Conclusion
(exemple \(\color{deeppink}{P}\) définie pour tout \(\color{dodgerblue}{n\geq 0}\))
J'écris que
\(P\) est vraie au rang \(0\)
et
\(\color{deeppink}{P}\) est héréditaire à partir du rang \(0\)
alors
par récurrence, \(\color{deeppink}{P}\) est vraie pour tout \(\color{dodgerblue}{n\geq 0}\) .
Autrement dit,
le raisonnement par récurrence permet de conclure que
quelque soit le nombre \(\color{dodgerblue}{n\in\mathbb{N}}\) ,
la propriété \(\color{deeppink}{P}\) est vraie.
SYNTHESE
①
Le raisonnement par récurrence se construit en 3 étapes
Etape 1 - Initialisation
Etape 2 - Hérédité
Etape 3 - Conclusion
②
Etape 1 - Initialisation
(exemple \(\color{deeppink}{P}\) définie pour tout \(\color{dodgerblue}{n\geq 0}\))
Je montre que \(\color{deeppink}{P}\) est vraie au rang \(n=0\).
③
Etape 2 - Hérédité
Je suppose que \(\color{deeppink}{P\big(\color{dodgerblue}{k}\big)}\) est vraie
et
je montre que \(\color{deeppink}{P\big(\color{dodgerblue}{k+1}\big)}\) est vraie.
④